あまりに問題が難しすぎて(ばかばかしくて)、もう笑うしかないことってありますよね。
この笑いってなんだろ。
手も足も出ない自分を第三者の視点から見て笑っちゃう(という英国紳士流のユーモア)が90%と
こんな問題を出題する奴(出題者)への笑いが10%かな。
その典型的なのがBlogに超難問マイクロソフトの入社試験(三角形の面積)で書いたやつかな
下の図の直角三角形の面積を求めよ、という問題(マイクロソフトの入社試験)なんだが。Blogでは
問題出しっぱなしだったので、こちらでちょっと解を考えてみた。
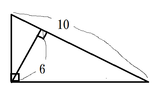
一瞬、なんやこれ30にきまっとるやんけ、と思うものの、
いや、待てよマイクロソフトがこんなに簡単な問題を出すわけがないよね、と思いなおす。
念のためにx,yの辺の長さを求めてみる。
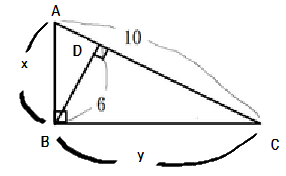
ピタゴラスの定理より
X2 + Y2 = 100 ・・・①
△ABC ∽ △ABD だから
X : 6 = 10 : Y
XY=60 ・・・②
①と②からXについてゴリゴリ解くと
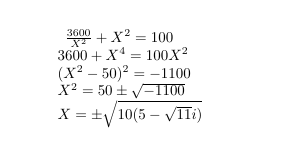
Mathmatica(Wolfram)に解かせると
In[2]:= Solve[{x*y==60, x*x+y*y==100},{x,y}]
Out[2]= {{x -> -Sqrt[10 (5 - I Sqrt[11])],
3/2
Sqrt[10] (5 - I Sqrt[11]) - 10 Sqrt[10 (5 - I Sqrt[11])]
> y -> -----------------------------------------------------------},
6
> {x -> Sqrt[10 (5 - I Sqrt[11])],
3/2
-(Sqrt[10] (5 - I Sqrt[11]) ) + 10 Sqrt[10 (5 - I Sqrt[11])]
> y -> --------------------------------------------------------------},
6
> {x -> -Sqrt[10 (5 + I Sqrt[11])],
3/2
Sqrt[10] (5 + I Sqrt[11]) - 10 Sqrt[10 (5 + I Sqrt[11])]
> y -> -----------------------------------------------------------},
6
> {x -> Sqrt[10 (5 + I Sqrt[11])],
3/2
-(Sqrt[10] (5 + I Sqrt[11]) ) + 10 Sqrt[10 (5 + I Sqrt[11])]
> y -> --------------------------------------------------------------}}
6
In[3]:=
実数の解はないから、この三角形は描けない。
一見、こういう三角形の図ができそうで描けない。
これがなりたつためにはBDが5以下でないといけない。
もしBD=5だった場合は二等辺三角形 X,Yの長さは
BD>5 だと角Bが90°未満にならざるを得ない。
これは三角形と外接円で考えると直感的にわかる。
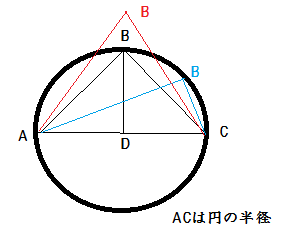
円の半径ACを底辺とし、円周上に頂点Bをもつ三角形を考える。黒い線の三角形と青い線の三角形の
角Bはいずれも直角になる。
このときBDが一番長いのは二等辺三角形(黒い線の三角形)になっているときであることは直感的にわかる。
この時BDは円の半径に等しい。これよりBDが長くとると、点Bは円の外側に出てしまうので角Bは90°未満に
ならざるを得ない(赤い線の三角形)。
ある意味、こういう問題って考えてみるといろんな示唆にとんでいて、難問というかジョークに近い問題だが
良問でもある。
平面上だと、こういう三角形は存在しないことになりますが
球面上だと存在する可能性があります。
球面上での考察は「マイクロソフトの三角形ありました」をご参照下さい。
また、球面上の三角形を考えるための数学的な準備は「続マイクロソフトの入社試験1」や
「球面上の三角形の考察」をご参照下さい。
◆入社試験関連のページ
お笑い2 ~面接の笑い話 GNPについて答えよ
マイクロソフトやGoogleの入社試験やってみた
◆英語
三角形の面積 triangle area
外接円 circumscrbed circle